En nybegynnerguide til binære trær

Hvis du har tatt et datastrukturkurs i informatikk-graden din, eller er en selvlært programmerer, er det sannsynlig at du har støtt på begrepet “Binary Trees”. Selv om de kan høres litt overveldende og komplekse ut, er konseptet med et binært tre ganske enkelt.

Les videre mens vi dissekerer binære trær, og hvorfor de er et nødvendig kjernekonsept for programmerere.

Hva er binære trær?

Binære trær er blant en av de første datastrukturer som studentene får undervisning i et datastrukturkurs. Et binært tre består av mange noder, og hver node i det binære treet inneholder to pekere som angir venstre og høyre barnedatanoder.

Den første noden i et binært tre kalles "roten". Noder på det siste nivået i et tre kalles blader.

Hver node inneholder et dataelement og to nodepekere. Et tomt binært tre er representert med en nullpeker. Som du kanskje allerede har funnet ut, kan binære trær bare ha to barn (derav navnet).

Typer binære trestrukturer

Det er flere forskjellige binære trestrukturer avhengig av måten nodene er plassert på. Et binært tre kalles et fullt binært tre når hver node i treet har enten null eller to barn. I et perfekt binært tre har alle noder to barn og bladene er alle på samme dybde.

I slekt: Beste måter å lære å kode gratis

Et komplett binært tre har noder fylt ut på hvert nivå, med unntak av det siste nivået. I komplette binære trær er noder konsentrert på venstre side av roten. En annen vanlig struktur er et balansert binært tre; i denne strukturen må høyden til høyre og venstre undertrær høyst variere med en. Det er også påkrevd at venstre og høyre undertrær også må balanseres.

Det er viktig å merke seg at høyden på det balanserte binære treet er O (logn), hvor n er antall noder i treet.

I noen tilfeller, hvis hver node bare har ett venstre eller høyre barn, kan det binære treet bli et skjevt binært tre. Den vil da oppføre seg som en lenket liste, slike trær kalles også et degenerert tre.

Hva er binære søketrær?

Et binært søketre (BST) er i hovedsak et ordnet binært tre med en spesiell egenskap kjent som egenskapen "binært søketre". BST -egenskapen betyr at noder med en nøkkelverdi mindre enn roten er plassert i venstre undertre, og noder med en nøkkelverdi som er større enn roten, er en del av det høyre undertreet.

BST -egenskapen må være sann for hver påfølgende overordnede node i treet.

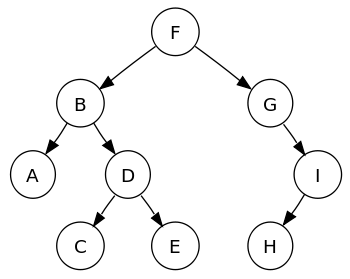
Binære søketrær tilbyr rask innsetting og oppslag. Innsetting, sletting og søkeoperasjoner har en kompleksitetstid i verste fall på O (n), som ligner på en koblet liste.

Fordeler med binære trær

Binære trær tilbyr mange fordeler, og derfor er de fortsatt en veldig nyttig datastruktur. De kan brukes til å vise de strukturelle forholdene og hierarkiene i et datasett. Enda viktigere er at binære trær tillater effektiv søk, sletting og innsetting.

Det er også veldig enkelt å implementere og vedlikeholde et binært tre. Et binært tre tilbyr programmerere fordelene med et bestilt utvalg og en koblet liste; søk i et binært tre er like raskt som i et sortert utvalg, og innsetting eller sletting er like effektivt som i koblede lister.

Binære trær er viktige datastrukturer

Binære trær er en veldig viktig datastruktur, og det er avgjørende at programmerere er komfortable med å bruke dem i programmene sine. Ofte spør intervjuere enkle binære treproblemer som traversals, maksimal dybde, speiling, etc.

Vi anbefaler på det sterkeste å forstå det binære trekonseptet, og å bli kjent med typiske intervjuproblemer.

TreeViz: En enkel måte å visualisere datastrukturer

Les neste

Om forfatteren