Hva er binær? [Teknologi forklart]

Annonse

Gitt at binær er så absolutt grunnleggende for datamaskinens eksistens, virker det rart at vi aldri har taklet det emnet før - så i dag hadde jeg trodd at jeg ville gi en kort oversikt over hva binær egentlig betyr og hvordan det brukes i datamaskiner. Hvis du alltid har lurt på hva forskjellen er mellom 8-bit, 32-bit, og 64-bit virkelig er det, og hvorfor det betyr noe - så les videre!

Hva er binært? Forskjellen mellom Base 10 og Base 2

De fleste av oss har vokst opp i en base med 10 tallverdener, og jeg mener at vi har 10 'utgangspunkt' tall (0-9) hvor vi henter alle andre tall. Når vi har brukt disse, går vi opp på enhetsnivå - 10-tallet, 100-tallet, 1000-tallet - denne formen for telling blir hamret inn i hjernen vår fra fødselen. Faktisk var det først fra romertiden at vi begynte å telle i base 10. Før det var base 12 den enkleste, og folk brukte knokene sine for å telle.

Når vi lærer base 10 på barneskolen, skriver vi ofte enhetene som dette:

Så tallet 1990 består faktisk av 1 x 1000

, 9 x 100, 9 x 10, og 0 x 1. Jeg er sikker på at jeg ikke trenger å forklare base 10 lenger enn det.

Men hva om i stedet for å ha et komplett utvalg av 0,1,2,3,4,5,6,7,8,9 å jobbe med som grunntall - hva om vi bare hadde hatt det 0, og 1. Dette kalles base 2; og det blir også ofte referert til som binær. I en binær verden kan du bare telle 0,1 - så må du gå til neste enhetsnivå.

Teller i binær

Det hjelper enormt hvis vi skriver ut enhetene når vi lærer binært. I dette tilfellet, i stedet for at hver ekstra enhet blir multiplisert med 10, blir den multiplisert med 2, noe som gir oss 1,2,4,8,16,32,64... Så for å hjelpe med å beregne, kan vi skrive dem ut slik:

Med andre ord representerer den høyeste verdien i et binært tall hvor mange 1er. Det neste sifferet, til venstre for det, representerer hvor mange to. Det neste representerer hvor mange 4-er… og så.

Med den kunnskapen kan vi skrive ut en tabell med teller i binær, med ekvivalent base 10-verdi angitt til venstre.

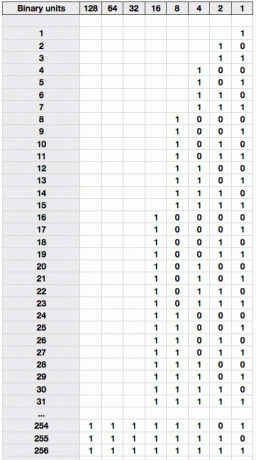
Bruk et øyeblikk på å gå over det til du kan se nøyaktig hvorfor 25 er skrevet som 11001. Du bør kunne bryte det ned som å være 16 + 8 + 1 = 25.

Arbeider bakover - base 10 til binær

Du skal nå kunne finne ut hvilken verdi et binært tall har ved å tegne en lignende tabell og multiplisere hver enhet. Å bytte et vanlig base 10-tall til binær tar litt mer krefter. Det første trinnet er å finne den største binære enheten som "passer inn" i tallet. Så hvis vi for eksempel klarte 35, så er det største tallet fra tabellen som passer inn i 35, så vi ville hatt en 1 der i den kolonnen. Vi har da en rest på 3 - som vil trenge en 2, og deretter til slutt en 1. Så vi får 100011.

8-bit, Bytes og Octets

Tabellen jeg har vist ovenfor er 8-bit, fordi vi maksimalt har 8 nuller og en til å bruke for vårt binære nummer. Dermed er det maksimale antallet vi muligens kan representere 11111111, eller 255. Dette er grunnen til å representere et hvilket som helst antall fra 0-255, vi trenger minst 8-bits. Octet og Byte er rett og slett en annen måte å si 8-bits på. Derfor 1 byte = 8 biter.

32 vs 64-biters databehandling

I dag hører du ofte begrepene 32-bit og 64-bit versjoner av Windows, og du vet kanskje at 32-biters Windows bare kan støtte opptil 4 gigabyte RAM. Hvorfor er det skjønt?

Det hele kommer ned til minneadressering. Hver minnebit trenger en unik adresse for å få tilgang til den. Hvis vi hadde en 8-bit minne adresseringssystem, ville vi bare ha maksimalt 256 byte minne. Med en 32-bit minne adresseringssystem (tenk deg å utvide tabellen over til å ha 32 binære enhetskolonner), kan vi dra hvor som helst opp til 4,294,967,296? 4 milliarder byte, eller med andre ord - 4 GIGAbytes.64-bit databehandling fjerner i hovedsak denne grensen ved å gi oss opp til 18 kvintillion forskjellige adresser - et antall de fleste av oss rett og slett ikke kan følge.

IPv4-adressering

Den siste bekymringen i dataverdenen er alt om IP-adresser IPv6 & The Coming ARPAgeddon [Technology Explained] Les mer , spesielt IPv4 adresser, som disse:

• 192.168.0.1
• 200.187.54.22

De består faktisk av 4 tall, som hver representerer en verdi opp til 255. Kan du gjette hvorfor? Jepp, hele adressen er representert av 4 oktetter (32 biter totalt). Dette virket som veldig mange adresser (rundt 4 milliarder faktisk) den gangen internett ble oppfunnet, men vi er raskt i ferd med å nå nå alt i livet vårt må kobles til. For å løse dette bruker den nye IPv6 128 biter totalt, noe som gir oss omtrent 340 undekillioner (satte 38 nuller på slutten) adresser å leke med.

Jeg kommer til å la det ligge der i dag, så jeg kan komme tilbake til det opprinnelige målet mitt, som var å skrive den neste Arduino-opplæringen - der vi i utstrakt grad bruker et bitskiftregister. Jeg håper i dag har gitt deg en grunnleggende forståelse av hvordan binær er så viktig for datamaskiner, hvorfor de samme tallene stadig vises, og hvorfor antallet biter vi har for å representere noe, setter en begrenset mengde minne, skjermstørrelse, mulige fargeverdier eller unike IP-adresser tilgjengelig for oss. Neste gang skal vi se på binære logikkberegninger, som er stort sett alt en datamaskinprosessor gjør, samt hvordan datamaskiner kan representere negative tall.

Kommentarer? Forvirring? Fant du forklaringen min lett å forstå? Uansett, ta kontakt med kommentarene. Jeg vil forlate deg med en binær vits!

Det er bare 10 typer mennesker i verden: de som forstår binær, og de som ikke gjør det.

Bildekreditt: Shutterstock