7 algoritmer alle programmerere burde vite

Som student i programmering har du sannsynligvis lært mange forskjellige algoritmer i løpet av karrieren. Å bli dyktig i forskjellige algoritmer er helt avgjørende for enhver programmerer.

Med så mange algoritmer kan det være utfordrende å holde styr på hva som er viktig. Hvis du forbereder deg på et intervju eller bare pusser opp ferdighetene dine, vil denne listen gjøre det relativt enkelt. Les videre mens vi viser de viktigste algoritmene for programmerere.

1. Dijkstra's algoritme

Edsger Dijkstra var en av de mest innflytelsesrike datavitenskaperne i sin tid, og han bidro til mange forskjellige områder innen databehandling, inkludert operativsystemer, kompilatorkonstruksjon og mye mer. Et av Dijkstras mest bemerkelsesverdige bidrag er oppfinnsomheten til hans korteste banealgoritme for grafer, også kjent som Dijkstra's Shortest Path Algorithm.

Dijkstras algoritme finner den korteste banen i en graf fra en kilde til alle grafhoder. På hver iterasjon av algoritmen legges et toppunkt med minimumsavstanden fra kilden og en som ikke eksisterer i den nåværende korteste banen. Dette er den grådige egenskapen som brukes av Djikstras algoritme.

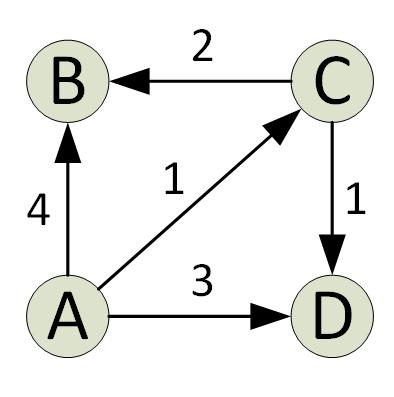
Algoritmen implementeres vanligvis ved hjelp av et sett. Dijkstras algoritme er veldig effektiv når den implementeres med en Min Heap; du kan finne den korteste banen på bare O (V+ElogV) tid (V er antall hjørner og E er antall kanter i en gitt graf).

Dijkstras algoritme har sine begrensninger; den fungerer bare på dirigerte og uorienterte grafer med kanter med positiv vekt. For negative vekter er Bellman-Ford-algoritmen vanligvis å foretrekke.

Intervjusspørsmål inkluderer vanligvis Djikstras algoritme, så vi anbefaler på det sterkeste å forstå dens intrikate detaljer og applikasjoner.

2. Slå sammen Sorter

Vi har et par sorteringsalgoritmer på denne listen, og sammenslåingssortering er en av de viktigste algoritmene. Det er en effektiv sorteringsalgoritme basert på programmeringsteknikken Divide and Conquer. I et verst tenkelig scenario kan sammenslåingssortering sortere "n" tall på bare O (nlogn) tid. Sammenlignet med primitive sorteringsteknikker som f.eks Boblesortering (det tar O (n^2) tid), sammenslåingssortering er utmerket effektiv.

I slekt: Introduksjon til flette sorteringsalgoritme

I sammenslåingssortering blir matrisen som skal sorteres, gjentatte ganger delt inn i underarrayer til hvert delarray består av et enkelt tall. Den rekursive algoritmen fusjonerer deretter delarrayene gjentatte ganger og sorterer matrisen.

3. Quicksort

Quicksort er en annen sorteringsalgoritme basert på programmeringsteknikken Divide and Conquer. I denne algoritmen blir et element først valgt som pivot, og hele matrisen blir deretter delt rundt denne pivoten.

Som du sikkert har gjettet, er en god pivot avgjørende for en effektiv sortering. Pivoten kan enten være et tilfeldig element, medieelementet, det første elementet eller til og med det siste elementet.

Implementeringer av quicksort er ofte forskjellige i måten de velger en pivot. I gjennomsnittlig tilfelle vil quicksort sortere et stort utvalg med en god pivot på bare O (nlogn) tid.

Den generelle pseudokoden for kvicksort deler partiet flere ganger på pivoten og plasserer den i riktig posisjon for delarrayen. Det plasserer også elementene som er mindre enn svinget til venstre og elementene større enn svinget til høyre.

4. Dybde Første søk

Depth First Search (DFS) er en av de første grafalgoritmene som ble undervist til elevene. DFS er en effektiv algoritme som brukes til å krysse eller søke i en graf. Den kan også modifiseres for å bli brukt i tretraversal.

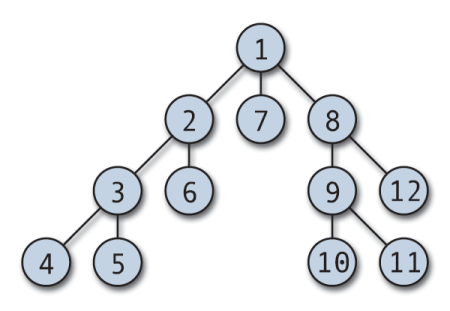
DFS -traversal kan starte fra en vilkårlig node, og den dykker ned i hvert tilstøtende toppunkt. Algoritmen går tilbake når det ikke er noe ubesøkt toppunkt, eller det er en blindvei. DFS implementeres vanligvis med en stabel og en boolsk matrise for å holde oversikt over de besøkte nodene. DFS er enkel å implementere og usedvanlig effektiv; det fungerer (V+E), hvor V er antall hjørner og E er antall kanter.

Typiske anvendelser av DFS -traversal inkluderer topologisk sortering, detektering av sykluser i en graf, banefinding og å finne sterkt tilkoblede komponenter.

5. Bredde-første søk

Breadth-First Search (BFS) er også kjent som en nivåordreoverføring for trær. BFS fungerer i O (V+E) som ligner på en DFS -algoritme. BFS bruker imidlertid en kø i stedet for stabelen. DFS dykker ned i grafen, mens BFS krysser grafen i bredden.

BFS -algoritmen bruker en kø for å holde oversikt over hjørnene. Ubesøkede tilstøtende hjørner blir besøkt, merket og i kø. Hvis toppunktet ikke har noen tilstøtende hjørne, fjernes et hjørne fra køen og utforskes.

BFS brukes ofte i peer-to-peer-nettverk, den korteste banen til en uvektet graf, og for å finne det minste spennetreet.

6. Binær søk

Binær søk er en enkel algoritme for å finne det nødvendige elementet i en sortert matrise. Det fungerer ved å gjentatte ganger dele matrisen i to. Hvis det nødvendige elementet er mindre enn det midtste elementet, behandles venstre side av det midterste elementet videre; ellers blir høyre side halvert og søkt igjen. Prosessen gjentas til det nødvendige elementet er funnet.

Den verste tidskompleksiteten til binært søk er O (logn), noe som gjør det veldig effektivt å søke etter lineære matriser.

7. Minimum algoritmer for spennende tre

Et minimum spantre (MST) i en graf har minimumskostnaden blant alle mulige spenningstrær. Kostnaden for et spennende tre avhenger av vekten på kantene. Det er viktig å merke seg at det kan være mer enn ett minimum som strekker seg over treet. Det er to hoved -MST -algoritmer, nemlig Kruskal og Prim.

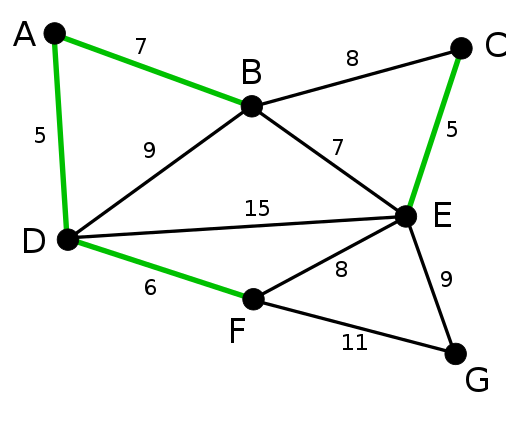
Kruskals algoritme lager MST ved å legge kanten med minimale kostnader til et voksende sett. Algoritmen sorterer først kanter etter vekten og legger deretter til kanter til MST ut fra minimum.

Det er viktig å merke seg at algoritmen ikke legger til kanter som danner en syklus. Kruskals algoritme er foretrukket for sparsomme grafer.

Prim's algoritme bruker også en grådig egenskap og er ideell for tette grafer. Den sentrale ideen i Prims MST er å ha to forskjellige sett med hjørner; ett sett inneholder den voksende MST, mens det andre inneholder ubrukte hjørner. På hver iterasjon velges minimumsvektkanten som vil koble de to settene.

Minste spennende tre -algoritmer er avgjørende for klyngeanalyse, taksonomi og kringkastingsnettverk.

En effektiv programmerer er dyktig med algoritmer

Programmerere lærer og utvikler stadig sine ferdigheter, og det er noen grunnleggende grunnleggende som alle trenger å være dyktige i. En dyktig programmerer kjenner de forskjellige algoritmene, fordelene og ulempene med hver, og hvilken algoritme som er mest passende for et gitt scenario.

En introduksjon til shell -sorteringsalgoritmen

Selv om skallsortering ikke er den mest effektive metoden, har nybegynnere mye å tjene på å praktisere den.

Les neste

Om forfatteren